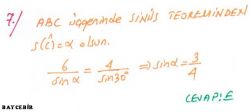Gür Yayınları Trigonometri Fasikülü Test 10

Üçgende Trigonometrik Bağıntılar  İle İlgili Sorular

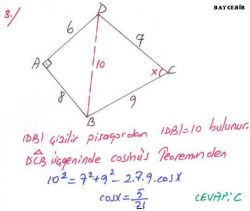
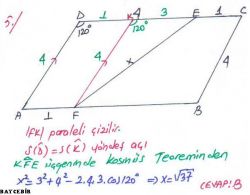
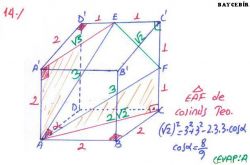
Kosinüs teoremi, geometride, üçgen üzerinde iki kenarı ve aralarındaki açı verilmiş iken bilinmeyen kenarı bulmak amacıyla kullanılan formüldür. Şekil 1'deki üçgene göre kosinüs teoreminin uygulanışı şöyledir:

Bir ABC üçgeninin kenar uzunlukları; a, b, c olmak üzere,

a² = b² + c² – 2 × b × c × cosA dır.

b² = a² + c² – 2 × a × c × cosB dir.

c² = a² + b² – 2 × a × b × cosC dir.

Kosinüs teoremi, iki kenar ve aralarındaki açı verildiğinde üçüncü kenarı bulmada ve üç kenar da verildiğinde açıları hesaplamada kullanılır. Ayrıca bu teorem, sadece dik üçgenlerde uygulanan Pisagor bağıntısını tüm üçgenler için geneller.

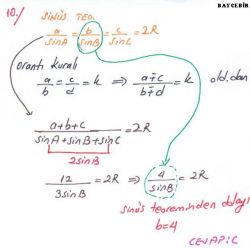
Sinüs teoremi

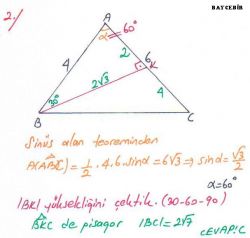
Sinüs teoremi, bir çembersel üçgende (kirişler üçgeni) bir kenar ve bu kenar karşısındaki açının sinüsleri oranı sabittir. Sinüs, dik açılı üçgenlerde dik olmayan bir açının karşısında kalan dik kenar ile hipotenüs (dik açının karşısında kalan kenar) ün birbirine oranıdır.

a, b, ve c üçgenin kenar uzunlukları, A, B ve C üçgenin iç açıları ve r çevrel çemberin yarı çapı ise bunlar arasında Sinüs teoremine göre aşağıdaki bağıntı mevcuttur.

a/SinA=b/SinB=c/SinC=2R