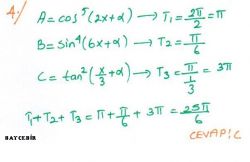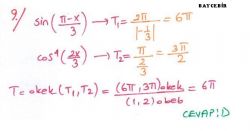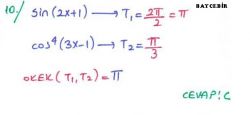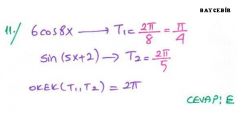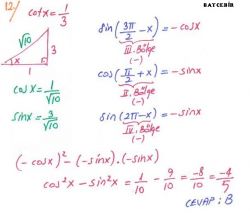Gür Yayınları Trigonometri Fasikülü Test 9
Peryodik Fonksiyon Ve Trigonometrik Fonksiyonların Grafiği İle İlgili Sorular
I. PERİYODİK FONKSİYONLAR
f, A kümesinden B kümesine tanımlı bir fonksiyon olsun.
f : A ® B
Her x Î A için f(x + T) = f(x)
olacak şekilde sıfırdan farklı en az bir T reel sayısı varsa; f fonksiyonuna periyodik fonksiyon, T ¹ 0 reel sayısına f nin periyodu denir. Bu eşitliği gerçekleyen birden fazla T reel sayısı varsa, bunların pozitif olanlarının en küçüğüne f fonksiyonunun esas periyodudenir.
f(x) in esas periyodu T ise, k tam sayı olmak üzere,
f(x) in periyodu k × T dir.
TRİGONOMETRİK FONKSİYONLARIN PERİYOTLARI
olduğu için sinx, cosx, tanx ve cotx fonksiyonları periyodiktir.
sinx ve cosx fonksiyonlarının periyodu 2kp, tanx ve cotx fonksiyonlarının periyodu kp dir.
sinx ve cosx fonksiyonlarının esas periyodu (k = 1 için) 2p; tanx ve cotx fonksiyonlarının esas periyodu p dir.
Kural
| a, b, c, d birer reel sayı ve m pozitif tam sayı olmak üzere,
f(x) = a + b × sinm(cx + d) g(x) = a + b × cosm(cx + d) fonksiyonlarının esas periyotları T olsun. Bu durumda,
olur. |
Kural
| a, b, c, d birer reel sayı ve m pozitif tam sayı olmak üzere,
f(x) = a + b × tanm(cx + d) g(x) = a + b × cotm(cx + d) fonksiyonlarının esas periyotları T olsun. Bu durumda,
|
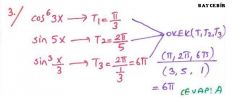
Kural
|
fonksiyonlarının esas periyodu, g(x) ve h(x) fonksiyonlarının esas periyotlarının en küçük ortak katına (e.k.o.k. una) eşittir. |
Uyarı
|
Buradaki kesirleri en sade biçimde olmalıdır. |
Uyarı
| f(x) = h(x) × g(x) olmak üzere, f(x) in esas periyodu, h(x) ve g(x) fonksiyonlarının esas periyotlarının en küçük ortak katına (e.k.o.k. una) eşit olmayabilir.
Eğer, f(x) = h(x) × g(x) in esas periyodu bulunacaksa, f(x) i fonksiyonların toplamı biçiminde yazarız. Sonrada toplanan fonksiyonların esas periyotlarının en küçük ortak katı alınır. Yukarıdaki açıklamalar bölünen fonksiyonlar için de geçerlidir. |
TRİGONOMETRİK FONKSİYONLAR ARASINDAKİ BAĞINTILAR
sin 2 x + cos 2 x = 1 tan x = sin x / cos x
tan x = 1/cot x cot x = cos x / sin x
cot x = 1/ tan x
TRİGONOMETRİK FONKSİYONLARIN İŞARETLERİ
1. Bölgede ( 0< x < 90° veya 0 < x < π/2 ) : sin + cos + tan + cot +
2. Bölgede ( 90° < x < 180° veya π/2 < x < π ) : sin + cos - tan - cot -
3. Bölgede ( 180° < x < 270° veya π < x < 3π/2 ) : sin - cos - tan + cot +
4. Bölgede ( 270° < x < 360° veya 3π/2 < x < 2π ) : sin - cos + tan - cot -